FAILURE CRITERIA
FAILURE CRITERIA
1 - Technical context
Predicting final failure in composite structures remains a challenge for design departments. In aeronautics and in rail transport, using composite materials under ever more severe conditions (temperatures, the presence of solvents and 3D geometry parts with ever greater thicknesses) may cause microcracks in parts with a composite structure. "The influence of microcracking on the performance and on the durability of composite structures still needs more work so as to properly understand and correctly predict changes in properties, thereby allowing certification bodies to tolerate the presence of microcracks in composite structures (Cinquin, March 2005)".
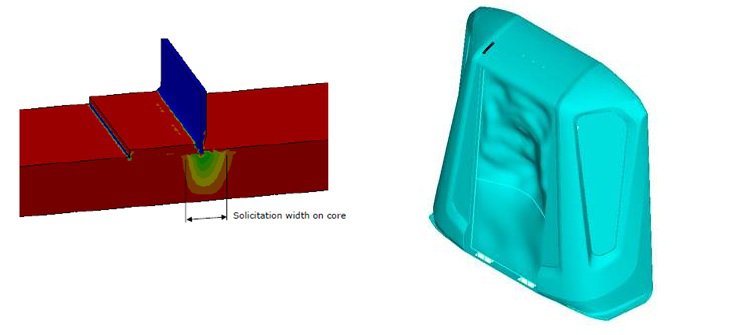
Analysing stresses in composites
2 - Failure criteria for composite materials
Failure criteria are mathematical expressions linking actual stresses present in the material with the ultimate stresses that the latter can bear. When these criteria are "violated" or exceeded, the material's integrity properties no longer exist and the environment is locally ruined. Most failure criteria for composites are said to be macroscopic. The reference scale is therefore that of a fold or layer.
The failure criteria for composite materials breakdown into two main families:
- So-called energy criteria
- So-called phenomenological criteria
Works linked to the World Wide Failure Exercise (WWFE 1998 and 2002) allowed some sorting to be done based on the many failure criteria developed for composites (min, max, stress or strain, Tsaï, Puck, Chamis, Rosen, Edge, Hart Smith, etc.) by revealing three batch criteria (modified Tsai Wu, Puck and Zinoviev).
2.1 - Polynomial criteria (energy or tensorial criteria)
Energy or tensorial criteria, the most well-known of which isthe Tsai Wu or Tsai Hill criterion (Tsai, 1992), are based on a generalisation of Von Mises-type plasticity criteria (Chevalier, Engineer's Techniques). As early as 1928, Von Mises put forwarda plasticity criterion for anisotropic bodies in the form of a quadratic expression of stress tensors. They were applied by Hill (Hill 1956) to the study of polycrystals. The drawback with energy criteria is that it is impossible to distinguish between composite failure modes. This limitation therefore excludes them from any future use after the first failures. Their use is however simplified by using a single value for predicting failure. "Most failure criteria are meaningless curves passed through unrelated data points," John Hart Smith.
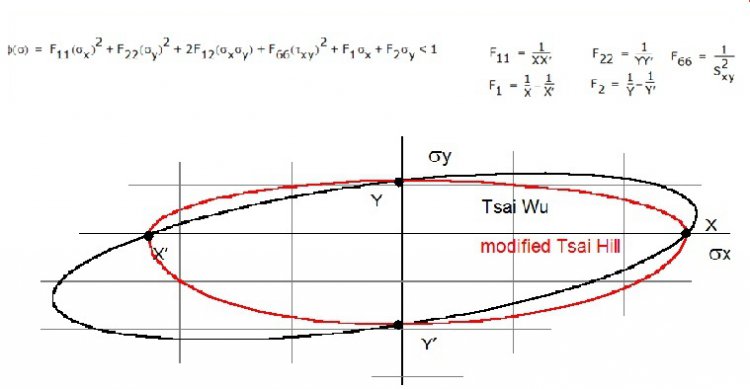
Tsai Wu criteria
2.2 - Phenomenological criteria
Phenomenological criteria, on the other hand, attempt to link a criterion with every failure mode. The oldest criterion is that of Hashin (Hashin, 1980). Theyapply to unidirectional composites and are based on four main failure modes induced by second order tensorial criteria. Hashin's criterion was improved by its author and has evolved. Puck's criterion (Puck, 1998 and Puck, 2002), for example, introduces the concept of a critical plane and a Coulomb's friction type model for compression/shear failures. Larc02 (Ragionieri, 2007) and then Larc03 (Davila and al., 2005) criteria detail and simplify the procedure used for obtaining parameters. In some ways, the Larc03 criterion is a more complete version of Puck's criterion. Six different failure criteria are set out.
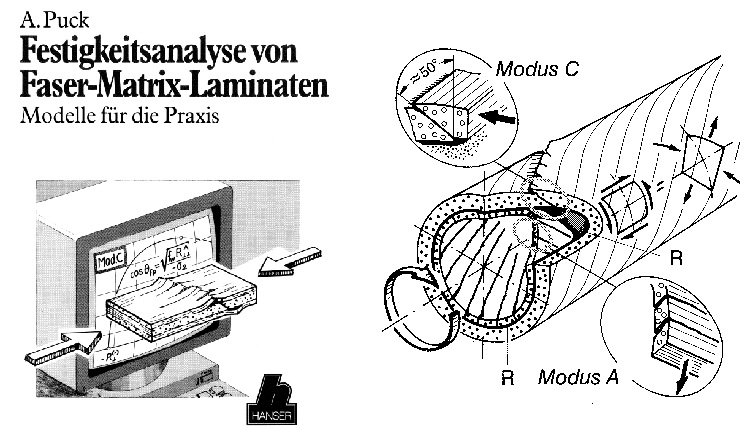
Puck's works
Using phenomenological criteria is more complex than using polynomial criteria as there is a need to determine the value of each criterion for every failure mode. This is however a necessary step when performing advanced composite simulations. This is because when behaviour that exceeds the first failure level is to be used, you need to start by detecting the initial damage using a phenomenological failure criteria, then go on to degrade characteristics in line with the determined failure.
3 - Behaviour beyond the first failures for composite materials
The behaviour beyond the initial layer failures results in a degradation of mechanical characteristics together with losses in rigidity. Losses in rigidity cause a reorganisation of the stresses in the part. Through some of its macroscopic aspects, this phenomenon may be compared with the plastic behaviour shown by metal materials. Often there is no consensus regarding the methods to be adopted for modifying the material after the initial failures.
The simplest of methods, and the one proposed by Tsai (Tsai, 1998), comprises of arbitrarily diminishing the transverse rigidities by a ratio of 85% and by 99% for fibre failures. This method leads to numerical instabilities linked to the lack of continuity and does not take into account the interactions between the different types of damage.
Damage mechanics, as developed in France for composites by Ladevèze (Ladeveze, 1989), introduce the notion of damage variables. These continuous variables are identified by specific tests after the initial failures. This approach has the advantage of being based on solid foundations that combine physics and thermodynamics, so as to allow explanations of the phenomena involved. The latest advancements made, known as mesomodels, have made it possible to introduce couplings between variables, to allow for delamination and also to allow for a link between micromechanics and mesomodels (Allixand al., 1998, Dublineauand al., 2002). The applications are promising ones, but the calculation times involved and the discrete nature of the meshing may however count against it when it comes to using it on industrial parts.
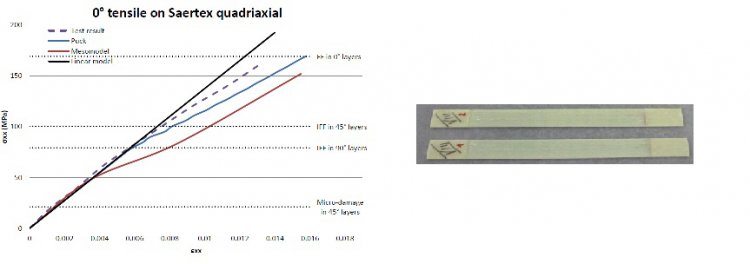
Comparing non-linear approaches for composite materials
Other methods comprise digital developments on specific finite elements: VCCT (Virtual Crack Closure Technique, O’Brien, 2001) for delaminating or more recently, EFM (Element Failure Method, Tay and al., 2008) which deals more generally with progressive failures.
Following on from WWFE, German teams worked around Puck's criterion in order to put forward a calculation method and tools covering the non-linear sizing domain. The culmination of this was the writing of VDI 2014 part 3 (Development of FRP components fibre-reinforced plastics analysis). This approach is an attractive one as it is close to that of a norm or standard (Lutz 2007). Its foundations allow it to envisage a generalisation of creep and fatigue domains. The material parameters are available for unidirectional layers, while the same work on woven layers has not yet been finalised.
4 - Coupling resistance/ageing
Composite materials are sensitive to the effects induced by the outside environment (temperature, humidity). The deteriorations caused by the environment are grouped under the heading of “aging” (Verdu, engineer's techniques).
When it comes to marine structures, one of the main couplings identified is the one between spreading humidity and damage (Mercier 2006). The presence of humidity diminishes the composite's vitreous transition temperature and its mechanical characteristics. Any damage may also change the humidity absorption kinetics by moving away from a classically Fickian behaviour. In the latter case, accelerations are observed in the deterioration phenomena (Sringer1981).
The reciprocal influence of fatigue and humidity damage has been little studied (Hai2000). Most of the time, a linear accumulation of the effects is done, without it being possible to extrapolate this approach to all materials. The most scientific approach would be to find evolution laws that apply to damage/humidity.
5 -Taking into account dispersion and reliability based sizing
Dispersion in composite material characteristics is a multi-level issue (at the fibre defect level, at the fibre distribution level in the matrix, as regards faults created during manufacture (orientation, porosities) and at the structural dimension level) (Guillauminat2008).
The probabilistic identification laws are often reduced to Weibull's model adapted to traction related behaviour in the fibre direction, even though in other directions other laws are more relevant (MIL HDB 17-1). Forecasting the mechanical reliability characteristics from fibre and resin component values has not yet resulted in a suitable theory. VER type approaches are often used with the known limits to resistance predictions (Dehmous2007).
Predicting dispersion effects linked to composite part manufacture is little studied. We can mention works around the RTM process (Guilleminot), but in most cases, as an example, dispersions relating to orientations are little known.
Taking into account the dispersion in mechanical characteristics when performing a structural calculation has, in France, been covered by many research works around the Americoproject run by DGA (Carrere 2008).
Lastly, for thick and large-size composite parts, the effects of these two levels on part reliability are known but rarely modelled (Gurvich, Pipe 1995).
6 - Bibliographic references
ADEME-CLAROM Séminaire Eoliennes Offshore, 2002, recueil des abstracts
ALLIX O., LADEVEZE P., GORNET L. LEVEQUE D. PERRET L. A computational damage mechanics approach for laminates Damage mechanics in engineering Materials Amsterdam, 1998.
CARRERE N. and all, Efficient structural computations with parameters uncertainty for composite applications, Composite Science and Technology 2008
CHAMIS C.C. Large Deformation Non-Linear Response of Composite Structures, NASA Workshop on FEM & FEA, 2000.
CHEVALIER Y. Les critères de rupture des composites - approchemacroscopique [Livre]. - [s.l.] : Techniques de l'Ingénieur. - A 7 755.
CHRISTENSEN R. M.« A critical evaluation for a class of micromechanics models ». J. Mech. Phys. Solids, 38 : 379-404, 1989.
CINQUIN J. EADS Internal stress and micro cracks in structural composite parts for aeronautical applications [Conférence] // JournéesNationales des Composites. - JournéesNationales des Composites Compiègne : [s.n.], mars 2005.
Composite Material Handbook [Livre]. - [s.l.] : MILITARY HANDBOOK 17-3F.
DEHMOUS Fiabilitéetmicromécanique des matériaux composites Application à la passerelle de Laroin, 2007, ThèseInstitut National Polytechnique de Toulouse
DAVILA C. G., CAMANHO P.P. AND ROSE C.A. "Failure Criteria for FRP Laminates" Journal of Composite Materials Vol39 n°4, 2005.
DUBLINEAU G. LADEVEZE P. On a damage mesomodel for laminates based on micromechanics Composite Science and Technology, vol62, 2002.
GURVICH, PIPE Strength size effect of laminated composite, 1995, Composite Science and Technology 55
GUILLAUMAT matériaux composites etfiabilité, 2008, présentation Clermont Ferrand
GUILLEMINOT Stochastic modeling of resin flow in fibrous media in liquid composite molding, 16th international conference on composite materials
HASHIN (Z.). – Failure criteria for unidirectional fiber composites ASME, J. Applied Mechanics, vol. 47, p. 329-334 (1980).
HILL Crutères de rupture des composites Techniques de l’IngénieurYvon CHEVALIER.
LADEVEZE P. About a damage mechanics approach, Mechanics and mechanisms of Composite and Multimaterials, MEP, 1989.
LARC03 Failure Criteria for FRP Laminates, C. G. Davila, P.P. Camanho and C.A. Rose Journal of Composite Materials, Vol39, n°4,
LUTZ Günther The Puck theory of failure in laminates in the context of the new guideline VDI 2014 Part 3, 2007, VULKANKupplungs- und Getriebebau
MACKENSIE DONALD ET WOOD JIM The Use of Finite element Analysis in Design by Analysis [Conférence]. - Paris : CCOPPS University of Strathclyde, 2008.
MERCIER J.Thèse Prise en compte du vieillissementet de l’endommagementdans le dimensionnement de structures en matériaux composites, 2006, Ecole des Mines de Paris
MILITARY HANDBOK 17-3 volume 3.polymer matrix composites materials usage, design, and analysis US Department of Defense.
MIYANO Y., NAKADA M. and CAI Formulation of long term creep and fatigue strength on ATM Strength and Life of Composites, Ed TSAI, 2008.
O’BRIEN K. Characterization, analysis and prediction of delamination in composites using fracture mechanics NASA Report, 2001.
PUCK A. SCHURMANN H Failure analysis of FRP laminates by means of physically based phenomenological models, Composites Sciences and Technology vol58 (1998).
PUCK A., KOPP J., KNOPS M. - Guidelines for the determination of the parameters in Puck’s action plane strength criterion, Composites Sciences and Technology vol62 (2002).
RAGIONIERI S. ET WEINBERG D. Finite Element implementation of advanced failure criteria for composites [Revue]. - [s.l.] :Noran Engineering, 2007.
SPRINGER Environmental Effects on Composite Materials, 1981, Technomic
TAY T-E, LIU G., SUN X., RIDHA M. TAN V. PHAM DC, PHAM THT Progressive failure analysis of composites Strength and Life of Composites Ed TSAI 2008.
TSAI S. LIU K-S A progressive quadratic failure criterion for a laminate – Composite Science and Technology vol 58 1998.
Z. HASHIN AND S. SHTRIKMAN. « A variational approach to the theory of the elastic behavior.
VDI 2014 Development of FRP components (fibre-reinforced plastics) Analysis 2006 VEREIN DEUTSCHER INGENIEURE
VERDU Vieillissementchimique des polymères, Techniques de L’ingénieur AM 3-152
WWFE World Wide Failure Exercise, HINTON, SODEN, KADDOUR Composite Science and Technology vol62 2002 et vol58 (1998).

