Optimisation topologique, ACS
-

définition volume de matière de travail (maximum alloué pour la pièce ou la structure)
-
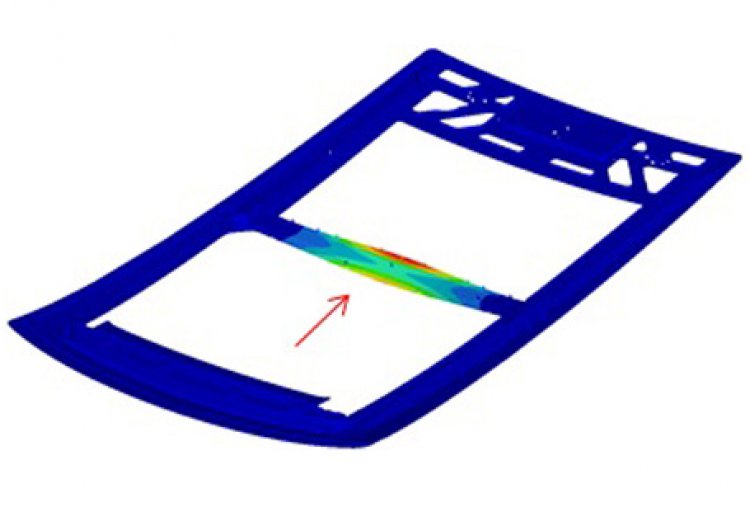
Calcul éléments finis avec algorithmes d’optimisation topologique. Objectif de réduction de masse. Contraintes de tenue mécanique sous charge et de fréquences propres de vibration élevées.
-
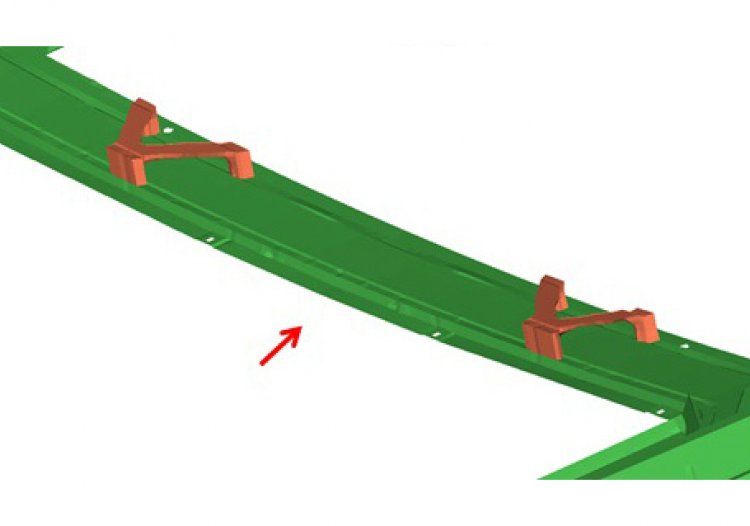
Définition d'un réseau nervure optimal
Utiliser la matière à bon escient, réduire la masse, réduire les coûts et ainsi définir de nouveaux concepts.
Dans un contexte de limitation des ressources naturelles, l’optimisation topologique s’impose comme un outil indispensable pour la conception des produits et structures
Calcul-Méca mène des études d’optimisation topologique.
Exemple de traverse en polymère injectée, soumise à un effort longitudinal en son centre. Non renforcée, la traverse subit une torsion trop importante.
Traditionnellement, l'ingénieur de bureau d'étude résout les problèmes de conception en procédant par essais successifs. A partir de son expérience et de son savoir-faire, il dessine une première pièce, puis, vérifie par le calcul qu'elle respecte le cahier des charges. Si ce n'est pas le cas, il modifie son dessin et ainsi de suite jusqu'au respect des contraintes. Dans la plupart des cas, plusieurs itérations sont nécessaires. Cette façon de faire est ainsi souvent très coûteuse en temps et imprécise.
L'optimisation topologique consiste à trouver la répartition de matière idéale dans un volume donné soumis à des contraintes mécaniques. Le problème à résoudre peut comporter de multiples contraintes (résistance, rigidité, tenue en fatigue, vibration, thermique, ..).
Une densité topologique variant entre 0 et 1 est attribuée à chacun des éléments de discrétisation (maillage éléments finis). Le problème est ensuite optimisé en utilisant une méthode de pénalités pour forcer les densités des éléments vers 0 (pas de matière) ou vers 1 (présence de matière).
L’optimisation topologique permet de définir de nouveaux concepts de structures ou de retrouver des concepts éprouvés (voir cas du pont). Il s'agit d'un outil de conception sans a priori, permettant de choisir une topologie initiale adéquate. Cela intervient, en avant-projet, comme une aide objective pour la sélection des caractéristiques générales de la structure.
Calcul-Méca utilise les outils d’optimisation Optistruct de la société Altair.

