CRITERES DE RUPTURE
CRITERES DE RUPTURE
1 - Contexte technique
La prévision de la rupture finale des structures composites reste un enjeu de challenge pour les bureaux d’études. Dans l’aéronautique et le transport ferroviaire, l’utilisation des matériaux composites dans des conditions de plus en plus sévères (température, présence de solvants, pièces de géométrie 3D avec des épaisseurs de plus en plus importantes) peut causer des microfissures dans les pièces de structures composites. « L’influence de la micro-fissuration sur les performances et la durabilité des structures composites nécessitent encore des travaux pour permettre de bien comprendre et de bien prévoir les évolutions des propriétés et ainsi permettre aux organismes de certification de tolérer la présence de micro-fissures dans le structures composites » (CINQUIN, mars 2005).
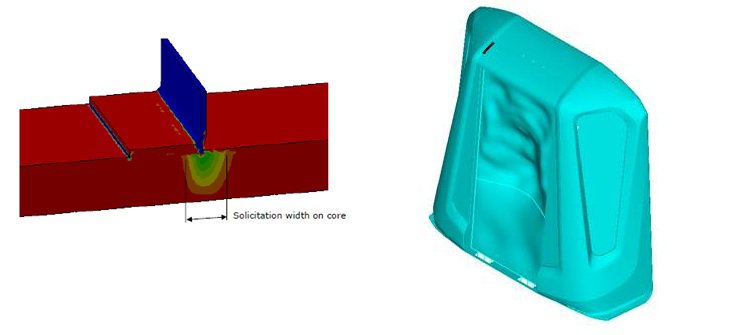
Analyse des contraintes dans les composites
2 - Critères de rupture pour matériaux composites
Le critère de rupture est une expression mathématique reliant les contraintes effectives régnant dans le matériau aux contraintes ultimes pouvant être supportées par ce dernier. Lorsque ce critère est « violé » ou dépassé, la propriété d’intégrité du matériau n’existe plus et il y a ruine locale du milieu. La grande majorité des critères de rupture pour les composites sont dits macroscopiques. L’échelle de référence est donc celle du pli ou de la couche.
Les critères de rupture pour les matériaux composites se décomposent en deux grandes familles :
- Les critères dits énergétiques,
- Les critères dits phénoménologiques.
Les travaux liés au World Wide Failure Exercise (WWFE 1998 et 2002) ont permis d’effectuer un certain tri sur les nombreux critères de ruptures développés pour les composites (min, max, stress ou strain, Tsaï, Puck, Chamis, Rosen, Edge, Hart Smith, etc.) en faisant ressortir 3 critères du lot (Tsaï Wu modifié, Puck et Zinoviev).
2.1 - Critères polynomiaux
Les critères énergétiques ou tensoriels, dont les plus connus sont les critères de Tsaï Wu ou Tsaï Hill (TSAI, 1992), sont basés sur une généralisation des critères de plasticité de type Von Mises (CHEVALIER, Techniques de l’Ingénieur). Dès 1928, Von Mises a proposé un critère de plasticité pour les corps anisotropes sous la forme d’une expression quadratique du tenseur des contraintes. Il a été appliqué par Hill (Hill 1956) à l’étude des polycristaux. L’inconvénient des critères énergétiques est de ne pas pouvoir distinguer les modes de ruptures des composites. Cette limitation les exclut donc pour une utilisation future après premières ruptures. Leur utilisation est par contre simplifiée par l’utilisation d’une valeur unique permettant de prévoir la rupture. "Most failure criteria are meaningless curves passed through unrelated data points" John Hart Smith.
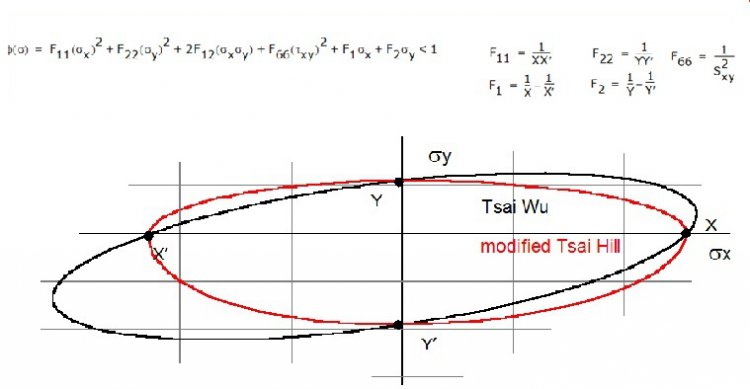
Critère de Tsaï Wu
2.2 - Critères phénoménologiques
Les critères phénoménologiques cherchent au contraire à mettre en relation un critère par mode de rupture. Le critère le plus ancien est celui d’Hashin (HASHIN, 1980). Il s’applique aux composites unidirectionnels et est basé sur quatre modes principaux de rupture du matériau induits par des critères tensoriels de rang 2.
Le critère d’Hashin a été amélioré par son auteur ou bien a connu des évolutions. Le critère de Puck (PUCK, 1998 et PUCK, 2002) introduit, par exemple, la notion de plan critique et de modèle de type frottement de Coulomb pour les ruptures en compression/cisaillement. Le critère de Larc02 (RAGIONIERI, 2007) puis Larc03 (DAVILA and al., 2005) précise et simplifie la procédure d’obtention des paramètres.
Par certains côtés, le critère Larc03 est une version plus complète du critère de Puck. 6 critères de rupture différents sont posés.
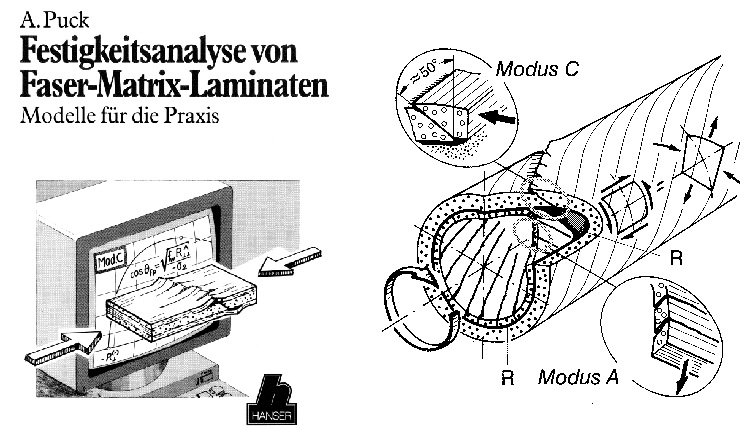
Travaux de Puck
L’usage des critères phénoménologiques est moins aisé dans son utilisation que les critères polynomiaux car il faut déterminer la valeur de chaque critère pour chaque mode de rupture. Ils sont cependant une étape nécessaire pour la simulation avancée des composites. En effet, pour permettre de prendre en compte un comportement au-delà des premières ruptures, il faut commencer par détecter le premier endommagement par un critère de rupture phénoménologique et, ensuite, dégrader les caractéristiques en fonction du mode de rupture déterminé.
3 - Comportement au-delà des premières ruptures pour les composites
Le comportement au-delà des premières ruptures de couches se traduit par une dégradation des caractéristiques mécaniques associée à des pertes de rigidité. Les pertes de rigidité provoquent une réorganisation des contraintes dans la pièce. Par certains aspects macroscopiques, ce phénomène peut être rapproché du comportement plastique des matériaux métalliques. Il n’y a pas toujours de consensus sur les méthodes à adopter pour modifier le matériau après premières ruptures.
La plus simple des méthodes, qui est celle proposée par Tsaï (TSAI, 1998), consiste à diminuer arbitrairement les rigidités transverses dans un rapport de 85% et de 99% pour les ruptures de fibres. Cette méthode conduit à des instabilités numériques liées à la discontinuité et ne tient pas compte des interactions entre les endommagements.
La mécanique de l’endommagement développée en France pour les composites par Ladevèze (LADEVEZE, 1989) introduit la notion de variables d’endommagement. Ces variables continues sont identifiées par des essais spécifiques après premières ruptures. Cette approche a l’avantage d’être basée sur des fondements solidesalliant physique et thermodynamique, elle permet des explications des phénomènes en jeu. Les derniers développements réalisés, connus sous le vocable de mésomodèle, ont permis d’introduire des couplages entre les variables, la prise en compte du délaminage ainsi qu’un lien entre micro-mécanique et mésomodèle (ALLIX and al., 1998, DUBLINEAU and al., 2002). Les applications sont prometteuses Les temps de calcul et la discrétisation du maillage peuvent par contre être pénalisants pour une réalisation sur pièces industrielles.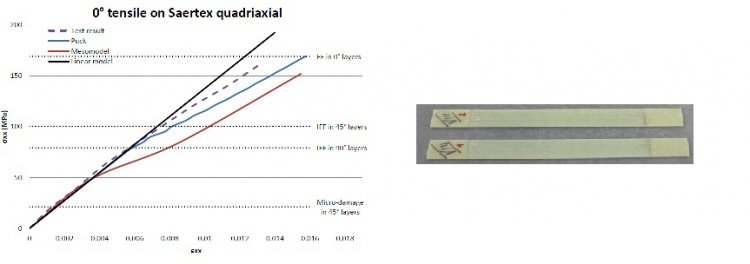
Comparaison des approches non-linéaires pour matériaux composites
D’autres méthodes consistent en des développements numériques sur des éléments finis particuliers : la méthode VCCT (Virtual Crack Closure Technique, O’BRIEN, 2001) pour le délaminage ou plus récemment l’approche EFM (ElementFailureMethod, TAY and al., 2008) plus générale sur la rupture progressive.
A la suite du WWFE, les équipes allemandes ont travaillé autour du critère de Puck, de manière à proposer une méthode de calcul et des outils couvrant le domaine du dimensionnement non-linéaire. L’aboutissement en a été la rédaction du VDI 2014 partie 3 (Development of FRP components fibre-reinforced plastics Analysis). L’approche est séduisante car proche d’une norme ou d’un standard (LUTZ 2007). Ses fondements lui permettent d’envisager une généralisation au domaine du fluage et de la fatigue. Les paramètres matériaux sont disponibles pour des couches unidirectionnelles, le même travail sur les couches tissées n’est par contre pas encore finalisé.
4 - Couplage résistance/vieillissement
Les matériaux composites sont sensibles aux effets de l’environnement extérieur (température, humidité). Les dégradations provoquées par l’environnement sont regroupées sous le vocable de vieillissement (VERDU, techniques de l’ingénieur).
Dans le domaine des structures marines, l’un des principaux couplages identifiés est celui entre la diffusion de l’humidité et l’endommagement (MERCIER 2006). La présence d’humidité diminue la température de transition vitreuse du composite et les caractéristiques mécaniques. La création d’endommagement peut aussi modifier la cinétique d’absorption d’humidité en s’éloignant d’un comportement classiquement Fickien. Dans ce dernier cas, des accélérations de phénomènes de dégradation s’observent (SRINGER 1981).
L’influence réciproque des endommagements en fatigue et de l’humidité a été peu étudié (HAI 2000). La plupart du temps, un cumul linéaire des effets est réalisé sans pour autant que la démarche soit extrapolable à tous les matériaux. L’approche la plus scientifique consisterait à trouver des lois d’évolution entre endommagement et humidité.
5 - Prise en compte de la dispersion, dimensionnement fiabiliste
La dispersion des caractéristiques des matériaux composites est un problème multi-échelle : échelle des défauts pour la fibre, échelle de la distribution des fibres dans la matrice, défauts créés par la fabrication (orientation, porosités), échelle des dimensions de la structure (GUILLAUMINAT 2008).
Les lois d’identification probabilistes sont souvent réduites au modèle de Weibull adapté au comportement en traction dans le sens des fibres bien que dans les autres directions d’autres lois soient plus pertinentes (MIL HDB 17-1). La prévision des caractéristiques mécaniques en fiabilité à partir des valeurs des constituants fibre et résine n’a pas encore trouvé de théorie adaptée. Les approches de type VER sont souvent utilisées avec les limites connues sur la prévision en résistance (DEHMOUS 2007).
La prévision des effets de dispersion liés à la fabrication des pièces composites n’est que peu étudiée. On peut citer les travaux autour du procédé RTM (GUILLEMINOT), mais dans la majeure partie des cas, les dispersions sur les orientations sont par exemple méconnues.
La prise en compte de la dispersion des caractéristiques mécaniques lors d’un calcul de structure a fait l’objet en France de nombreux travaux de recherche autour du projet AMERICO de la DGA (CARRERE 2008).
Enfin pour les pièces composites épaisses et grandes dimensions, les effets de ces deux échelles sur la fiabilité des pièces sont connus mais peu modélisés (GURVICH, PIPE 1995).
6 - Références bibliographiques
ADEME-CLAROM Séminaire Eoliennes Offshore, 2002, recueil des abstracts
ALLIX O., LADEVEZE P., GORNET L. LEVEQUE D. PERRET L. A computational damage mechanics approach for laminates Damage mechanics in engineering Materials Amsterdam, 1998.
CARRERE N. and all, Efficient structural computations with parameters uncertainty for composite applications, Composite Science and Technology 2008
CHAMIS C.C. Large Deformation Non-Linear Response of Composite Structures, NASA Workshop on FEM & FEA, 2000.
CHEVALIER Y. Les critères de rupture des composites - approche macroscopique [Livre]. - [s.l.] : Techniques de l'Ingénieur. - A 7 755.
CHRISTENSEN R. M.« A critical evaluation for a class of micromechanics models ».J. Mech. Phys. Solids, 38 : 379-404, 1989.
CINQUIN J. EADS Internal stress and micro cracks in structural composite parts for aeronautical applications [Conférence] // Journées Nationales des Composites. - Journées Nationales des Composites Compiègne : [s.n.], mars 2005.
Composite Material Handbook [Livre]. - [s.l.] : MILITARY HANDBOOK 17-3F.
DEHMOUS Fiabilité et micromécanique des matériaux composites Application à la passerelle de Laroin, 2007, Thèse Institut National Polytechnique de Toulouse
DAVILA C. G., CAMANHO P.P. AND ROSE C.A. "Failure Criteria for FRP Laminates" Journal of Composite Materials Vol39 n°4, 2005.
DUBLINEAU G. LADEVEZE P. On a damage mesomodel for laminates based on micromechanics Composite Science and Technology, vol62, 2002.
GURVICH, PIPE Strength size effect of laminated composite, 1995, Composite Science and Technology 55
GUILLAUMAT matériaux composites et fiabilité, 2008, présentation Clermont Ferrant
GUILLEMINOT Stochastic modeling of resin flow in fibrous media in liquid composite molding, 16th international conference on composite materials
HASHIN (Z.). – Failure criteria for unidirectional fiber composites ASME, J. Applied Mechanics, vol. 47, p. 329-334 (1980).
HILL Crutères de rupture des composites Techniques de l’Ingénieur Yvon CHEVALIER.
LADEVEZE P. About a damage mechanics approach, Mechanics and mechanisms of Composite and Multimaterials, MEP, 1989.
LARC03 Failure Criteria for FRP Laminates, C. G. Davila, P.P. Camanho and C.A. Rose Journal of Composite Materials, Vol39, n°4,
LUTZ Günther The Puck theory of failure in laminates in the context of the new guideline VDI 2014 Part 3, 2007, VULKANKupplungs- und Getriebebau
MACKENSIE DONALD ET WOOD JIM The Use of Finite element Analysis in Design by Analysis [Conférence]. - Paris : CCOPPS University of Strathclyde, 2008.
MERCIER J. Thèse Prise en compte du vieillissement et de l’endommagement dans le dimensionnement de structures en matériaux composites, 2006, Ecole des Mines de Paris
MILITARY HANDBOK 17-3 volume 3.polymer matrix composites materials usage, design, and analysis US Department of Defense.
MIYANO Y., NAKADA M. and CAI Formulation of long term creep and fatigue strength on ATM Strength and Life of Composites, Ed TSAI, 2008.
O’BRIEN K. Characterization, analysis and prediction of delamination in composites using fracture mechanics NASA Report, 2001.
PUCK A. SCHURMANN H Failure analysis of FRP laminates by means of physically based phenomenological models, Composites Sciences and Technology vol58 (1998).
PUCK A., KOPP J., KNOPS M. - Guidelines for the determination of the parameters in Puck’s action plane strength criterion, Composites Sciences and Technology vol62 (2002).
RAGIONIERI S. ET WEINBERG D. Finite Element implementation of advanced failure criteria for composites [Revue]. - [s.l.] :Noran Engineering, 2007.
SPRINGER Environmental Effects on Composite Materials, 1981, Technomic
TAY T-E, LIU G., SUN X., RIDHA M. TAN V. PHAM DC, PHAM THT Progressive failure analysis of composites Strength and Life of Composites Ed TSAI 2008.
TSAI S. LIU K-S A progressive quadratic failure criterion for a laminate – Composite Science and Technology vol 58 1998.
Z. HASHIN AND S. SHTRIKMAN. « A variational approach to the theory of the elastic behavior.
VDI 2014 Development of FRP components (fibre-reinforced plastics) Analysis 2006 VEREIN DEUTSCHER INGENIEURE
VERDU Vieillissement chimique des polymères, Techniques de L’ingénieur AM 3-152
WWFE World Wide Failure Exercise, HINTON, SODEN, KADDOUR Composite Science and Technology vol62 2002 et vol58 (1998).

