Elastomères
COMPORTEMENT DES ELASTOMERES
La mise en charge cyclique d’une structure élastomérique met en jeu plusieurs phénomènes complexes qui peuvent éventuellement être couplés :
- Tout d’abord, le comportement hyperélastique non linéaire du matériau,
- L’accommodation du matériau (assouplissement après plusieurs cycles),
- Le raidissage dû à la fréquence de sollicitation,
- L’échauffement interne du matériau dû à l’hystérésis du comportement,
- Le fluage ou relaxation de la structure,
- Enfin la fatigue du matériau due à ces sollicitations cycliques.
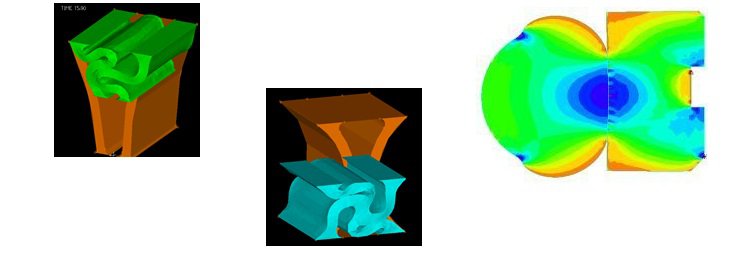
Calcul de pièces en élastomères
1 - Comportement hyperélastique du matériau
Si la pièce à analyser est une structure à base de caoutchouc, son comportement en statique peut se modéliser à l’aide de lois hyperélastiques (GENT, 1958). En fonction du taux de déformation que l’on peut atteindre dans la structure, plusieurs formes de lois peuvent être utilisées (Néo-Hooke, Mooney-Rivlin, Ogden, Arruda-Boyce,…) (ARRUDA, 1993). Le choix du potentiel hyperélastique est à effectuer au moment de la modélisation, après analyse d’essais mécaniques réalisés sur éprouvettes.
Il convient de noter que ces essais doivent être de natures différentes (en terme d’invariants de la déformation), de manière à couvrir un large domaine de multi-axialité. Généralement, il est recommandé d’effectuer des essais de traction uni-axiale, des essais de compression ou de traction équibiaxiale et des essais de cisaillement.

Essais de caractérisation de matériaux élastomères
Des essais de compressibilité sont en général également réalisés. En effet, même si les matériaux élastomères sont réputés incompressibles, ils ne le sont jamais complètement, tout dépend du niveau de compression appliqué.
2 - Accomodation (ou effet Mullins)
Il s’agit de l’aptitude des matériaux à «mémoriser» le niveau maximal d’énergie atteint (TRELOAR, 1975). Pratiquement, dans une structure élastomère, même si initialement les caractéristiques matériaux sont identiques en tous points, après une mise en sollicitation, l’histoire vue par les éléments de matière sera différente. Ainsi, leurs lois de comportement sont différentes après quelques cycles.
Il est possible de modéliser cette accommodation à partir des données tirées des essais mécaniques (cf. modèle de Ogden-Roxburg). Il faut alors réaliser des essais mécaniques cyclés à différents niveaux de contraintes.
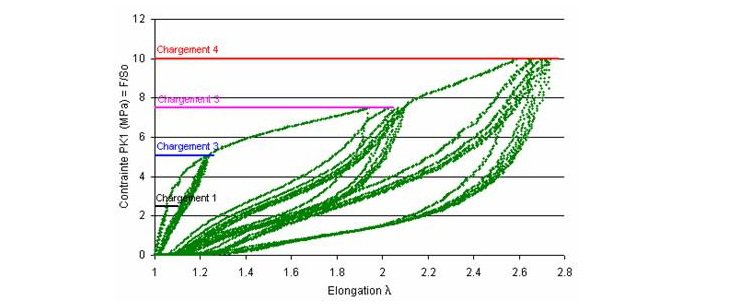
Illustration de l'effet Mullins
3 - Raidissage dû à la fréquence de sollicitation
La nature visqueuse des matières élastomères, leur confère un comportement dynamique analogue à celui d’un amortisseur. La fréquence et la sollicitation (notamment dans le cas de vibrations), peuvent entraîner un raidissage du matériau. Toutefois, on peut tenir compte de cet effet, en effectuant les essais matériaux aux fréquences de sollicitation.
4 - Échauffement interne
La nature visqueuse de ces matières leur confère également un comportement hystérétique. Cette différence de comportement entre le chargement et le déchargement, provoque une perte d’énergie dans le matériau qui se transforme en chaleur. Leur nature isolante peut alors «piéger» cette chaleur et entraîner une divergence thermique (surchauffe).
On notera également qu’une augmentation de température risque également d’accélérer le vieillissement/fluage/relaxation précisément dans les zones les plus contraintes.
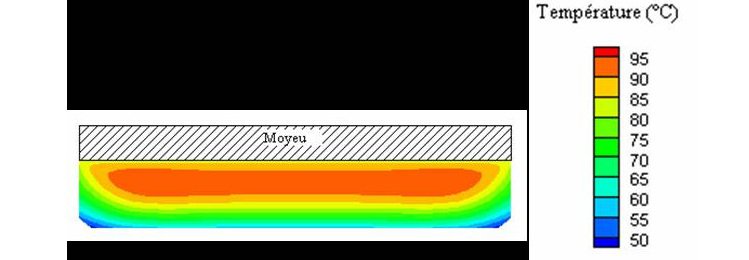
Échauffement interne d'un bandage de roue en élastomère
5 - Fluage ou relaxation de la structure
Le comportement visqueux des élastomères entraîne une perte de rigidité du matériau sous l’application d’une charge statique. Dans les matériaux hyperélastiques, cette perte de rigidité est fonction du niveau d’énergie dans le matériau (HOLZAPFEL, 1996). C’est la raison pour laquelle on se doit de réaliser des essais mécaniques de fluage (ou de relaxation) pour différents niveaux de contraintes (ou de déformation). Comme dans la partie «comportement hyperélastique», ces essais doivent être conduits en toute rigueur avec différents niveaux de multiaxialité (HOLZAPFEL, 2000 et 2001).
6 - Fatigue
Comme dans tous les matériaux, la présence de défauts (inévitables) dans une structure soumise à des sollicitations cycliques permet de propager ces défauts jusqu’à la ruine de la structure. Aujourd’hui, les modèles proposés par certains auteurs : Mars, Saintier, Verron, Layouni, Gruand,..., (MARS, 2001 et 2004 ; SAINTIER, 2001 ; GRUAND, 2006) ne font pas encore l’unanimité, même si cela ouvre des voies de recherche. L’efficacité des formulations reste encore à prouver (quand elles sont accessibles donc non confidentielles).
On pourra toutefois noter que le comportement en fatigue de ces matériaux est très dépendant de la température de fonctionnement. Ainsi, si l’on souhaite avoir une idée du comportement en fatigue, il faut passer par des essais mécaniques avec plusieurs niveaux d’énergies et plusieurs températures d’essais (idéalement et afin de couvrir un plan d’invariants, comme dans le cas statique, il faudrait également avoir recours à des essais différents).
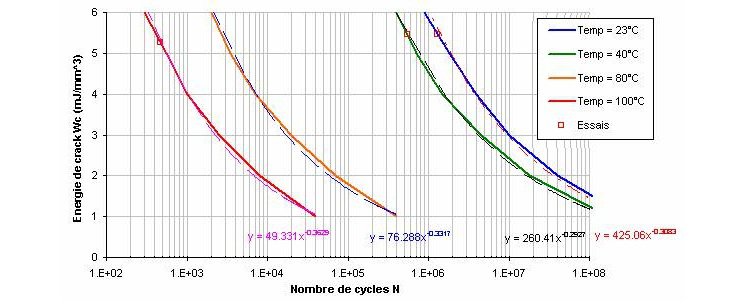
Approche en fatigue par énergie de crack
7 - Couplages
Enfin, tous ces phénomènes peuvent également être couplés. La température agit sur la rigidité des matériaux, accélérant le fluage, accélérant la fatigue, etc. Le fluage modifie la rigidité du matériau, modifiant ainsi la réponse de la structure devant les sollicitations et donc modifiant le comportement thermique de la structure etc.
8 - Références bibilographiques
ARRUDA E.M. AND BOYCE M. C., "A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials", J. Mech. Phys. Solids, Vol. 41 (2), pp 389-412 (1993).
ELASTOMER CRITERIA FOR ENGINEERING DESIGN, Edited by C Hepburn and R.J.Reynolds, Applied science publishers.
GENT AND THOMAS, "Forms of the stored strain energy function for vulcanized Rubber", J. Polym Sci., Vol. 28, pp. 625-637, 1958.
HOLZAPFEL G. A., "On large strain viscoelasticity: continuum formulation and finite element applications to elastomeric structures", Int. J. Num. Meth. Engng., Vol. 39, pp 3903-3926, 1996.
HOLZAPFEL G. A, "Nonlinear solid mechanics. A continuum approach for engineering". John Wiley & Sons, Chichester, pp 278-295, 2000.
HOLZAPFEL G. A, "Biomechanics of soft tissue", in Lemaitre (ed.), Handbook of Materials Behavior Models: Nonlinear Models and Properties, Academic Press, 2001, pp 1057-1071.
LAIARINANDRASANA L., MUNERA D. D ET GRUAND R. Creep damage mechanisms and fracture mechanics applied on aged and non aged polyamide 66 [Revue]. - Rolduc Abbey, Kerkrade, The Netherlands : [s.n.], 2006. - Vol. 13th International Conference on Deformation, Yield and Fracture of Polymers.
MARS W.V., 08-2001, Dissertation, Multiaxial fatigue of rubber.
MARS W.V.Multiaxial fatigue crack initition in rubber, Tire science and technology, TSTCA, Vol 29, n°3, July September 2001, pp 171-185.
MARS AND FATEMI "A novel specimen for investigating the mechanical behaviour of elastomers under multiaxial loading conditions, Society for experimental mechanics, page 136-146, vol 44, n°2, 04/2004.
SAINTIER N. Fatigue multiaxiale dans un élastomère de type NR charge : mécanismes d'endommagement et critère local d'amorçage de fissure, thèse 2001.
TRELOAR L.R.G, 3rd edition, the physics of Rubber elasticity, Clarendon Press Oxford, 1975.

