Composites : Prévision des caractéristiques
PRÉVISION DES CARACTÉRISTIQUES DES MATÉRIAUX COMPOSITES
1 - Contexte technique
Les matériaux composites se distinguent par une grande diversité de comportements issue de l’association des fibres et de la résine. La proportion de fibres, le type de renfort, l’orientation, sont autant d’éléments déterminants qui peuvent conduire à des matériaux aux caractéristiques complètement différentes. Il est ainsi possible d’obtenir à un matériau haute performance rigide, au comportement élastique fragile (longeron en pré-imprégné époxy/fibre de carbone) ou bien un matériau souple acceptant de fortes déformations (capotage en composite polyester/mat de fibre de verre).

Renfort à base de fibre de Carbone/Aramide/Verre (source Saertex)
Les matériaux composites présentent aussi la particularité de l’anisotropie : un comportement différent suivant les directions de sollicitation. Cette propriété physique augmente de manière importante le nombre de paramètres déterminant la rigidité, la résistance, la thermique, etc. (en général, au minimum 3 modules d’élasticité, 3 coefficients de Poisson et 3 modules de cisaillement).
Le nombre de combinaisons permettant de former des matériaux composites est quasi infini. Les matériaux composites sont ainsi développés sur-mesure.
Ces éléments expliquent pourquoi l’approche de type normalisation, existant pour les matériaux métalliques, a toujours été vaine pour les matériaux composites. Dans la pratique actuelle des bureaux d’études, les caractéristiques mécaniques des composites sont encore bien souvent issues de campagnes d’essais de caractérisation. De nombreux essais de caractérisation longs et coûteux doivent alors être effectués afin de développer des matériaux composites répondant aux cahiers des charges. En outre, dans bien des cas, les essais de caractérisation ne peuvent donner qu’une partie des caractéristiques d’un matériau. En effet, certains essais, comme les essais de compression, sont difficiles à mettre en œuvre et à interpréter.
Méca a développé, de manière complémentaire ou alternative aux essais, une approche par prévision des caractéristiques mécaniques des matériaux composites.

Différentes pièces en matériaux composites
2 - Etat de l'art dans le domaine de la micro-mécanique
2.1 - Les méthodes de prédiction de caractéristiques mécaniques
Le passage de l’échelle microscopique à l’échelle macroscopique figure parmi l’un des plus grands défis de la mécanique, mais également de l’ensemble des disciplines (optique, acoustique, etc.) constituant la physique générale moderne. En effet, les relations liant les agencements atomiques aux propriétés mécaniques macroscopiques d’une structure ne sont pas encore connues. Néanmoins, la connaissance la plus fine possible de la structure d’hétérogénéité d’un matériau permet, au prix de « raccourcis phénoménologiques » et de traitements d’ « homogénéisation », de déterminer un comportement macroscopique homogène, susceptible d’être par la suite intégré dans une formulation classique des milieux continus (GUILLEMINOT, 2008).

Arrangements réels des fibres et modèles théoriques
Les techniques d’homogénéisation ont été développées pour les matériaux composites. Il s’agit, à partir de la connaissance de la microstructure (fibre et résine seules), de déterminer le comportement du matériau ainsi réalisé.
Deux approches cohabitent (JONES, 1998) :
- La technique dite de la micromécanique, pour laquelle les relations sont exprimées de manière explicite sous forme de règles ou formules ;
- La technique dite du Volume Elémentaire Représentatif (VER*), plus générale et basée sur une simulation numérique, en général, par éléments finis d’un élément représentatif de matière.
Les fondements des techniques d’homogénéisation ont été posés d’un point de vue mathématique (NEMAT 1993). La résolution du problème de l’inclusion par Sir Eshelby en 1957 a permis sa formalisation sous forme tensorielle (ESHELBY, 1957). Le « lemme de Hill », les « bornes basses et hautes de Voigt et Reuss » ou plus récemment les « bornes de Hashin et Shtrikman »(BORNET, et al., 2001) permettent d’encadrer les valeurs prédites mais ne les évaluent pas.
De plus, la technique du VER* nécessite un nombre élevé de micro-constituants qui soit représentatif, statistiquement, des propriétés continues locales (GUILLEMINOT, 2008), ce qui est très difficile à définir et à obtenir.
2.2 - La prévision des caractéristiques de rigidité des matériaux composites :
Les modèles existants pour prévoir les caractéristiques de rigidité des matériaux sont basés en général sur des géométries simples et reproductibles (UD unidirectionnel, la fibre courte et l’inclusion sphérique).
2.2.1 - Cas des fibres longues :
Modèle de COX
Dans le premier modèle de prévision de la rigidité dans le sens des fibres (KOLLAR, et al., 2003), la fibre et la résine sont définies comme deux ressorts pouvant agir suivant un modèle série ou parallèle. Le transfert des charges s’effectue par cisaillement à l’interface suivant le modèle ShearLag (COX, et al., 1952). Les fibres sont alors dites longues et continues. La prévision au premier ordre des modules d’élasticité des couches de type unidirectionnelles pour les composites structuraux obéit globalement à cette loi (écart de -10% sur le module dans le sens des fibres pour des composites de type aéronautique). Dans le sens transverse aux fibres, des lois semi-empiriques ont été développées par Halpin-Tsai pour permettre d’obtenir une meilleure prévision des modules d’élasticité transverses, de cisaillement et des coefficients de Poisson (HALPIN, 1969). La prédictibilité de ces modèles est faible notamment pour les forts taux de fibres où les modèles surestiment les modules transverses aux fibres dans le sens de l’épaisseur.
2.2.2 - Cas des fibres courtes :
Pour les fibres courtes et les charges avec un faible taux de renfort (utilisées notamment en injection plastique), les rigidités peuvent être évaluées à partir du modèle de Mori Tanaka (MORI, et al., 1973). Le modèle de Lielens (DRAY BENSAHKOUM, 2006) permet d’améliorer les prédictions pour les fortes concentrations (typiquement 40% à 60%).
Il est également possible d’utiliser des évolutions autour de la méthode d’Eshelby, suivant des hypothèses différentes sur le milieu de référence : schéma dilué, schéma auto-cohérent et le modèle différentiel (Mc LAUGHLIN, 1977). Ce dernier consiste à ajouter successivement une faible fraction volumique de renforts au matériau homogénéisé, jusqu’à obtenir la fraction réelle dans le composite.
Les techniques d’homogénéisation par VER connaissent actuellement un nouveau souffle par l’intermédiaire des travaux de Ha (HA et HUANG, 2008). Ces derniers systématisent le calcul par éléments finis sur des VER. Ils incluent un nombre important de fibres couplé à l’approche de Miyano (MIYANO, 2008) sur la prévision des caractéristiques en fluage et température à partir des données mesurées sur la résine seule.
L’amélioration de la prédictibilité des modèles nécessite de mieux prendre en compte la réalité physique de l’organisation du renfort et de la matrice par rapport à une idéalisation géométrique et mathématique. Il est ainsi nécessaire d’étudier la prise en compte :
- Des porosités ou vides,
- Des contraintes liées à la fabrication,
- Des désalignements de renforts,
- Des micro-défauts (micro-fissurations), etc.
Dans le domaine des polymères injectés fibres courtes, des avancées importantes dans l’utilisation de la technique du VER et du modèle de Mori-Tanaka ont été effectuées autour de la suite du logiciel Digimat (DIGIMAT 2011). L’interfaçage avec les logiciels de rhéologie et de calcul a été réalisé. Les premiers retours d’expériences montrent que ces approches donnent des résultats très satisfaisants dans le domaine de la prévision des caractéristiques de rigidités (DRAY BENSAHKOUM, 2006) avec cependant un temps de résolution restant à optimiser.
Dans le domaine de la prévision des caractéristiques de rupture, les approches ne sont actuellement que qualitatives et restent à développer.
2.2.3 - Comportement non linéaire :
Le comportement non-linéaire des matériaux composites est essentiellement observé en cisaillement dans le plan et en compression transverse. Il est important de connaître ces évolutions afin de reproduire le phénomène de redistribution des contraintes jusqu’à rupture.
L’approche courante est issue de la mécanique de l’endommagement (MAIRE 2011). L’évolution des modules est alors reliée à celle d’un endommagement qui peut se visualiser sous la forme par exemple de microfissurations. Dans sa version simple non couplée, on retrouve le modèle type de Chaboche ou dans son évolution la plus raffinée celui des travaux de Ladeveze (LADEVEZE 2008).
L’approche semi-empirique d’évolution de la rigidité transverse d’un composite en cisaillement et en traction en lien avec le critère de Puck (Deuschle 2010) est une voie prometteuse car formant un ensemble très cohérent de méthodes et d’outils.
Des travaux expérimentaux récents ont mis en évidence que les non-linéarités notamment en cisaillement n’étaient pas seulement dues aux microfissurations mais comportaient aussi une part de plasticité. Des modèles couplés combinant mécanique de l’endommagement et plasticité sont en cours de développement (SHUECKER 2008).
2.3 - La prévision des caractéristiques de rupture des matériaux composites
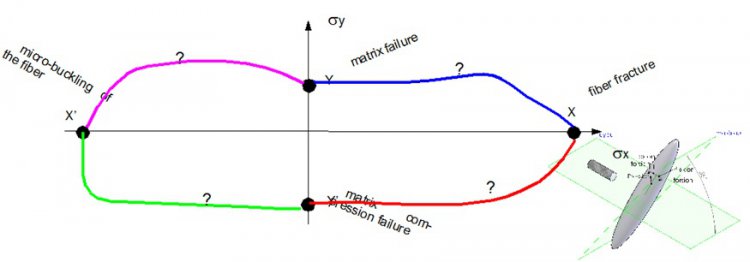
Enveloppe de rupture - couche unidirectionnelle fibres longues
Les caractéristiques de premières ruptures à déterminer, pour un composite stratifié ayant un comportement de type contraintes planes, sont au nombre de 5 (CHRISTENSEN, 1989) :
- Résistance dans le sens des fibres X en traction et X’ en compression,
- Résistances transverses aux fibres en traction Y, compression Y’ et le cisaillement plan S.
Ces résistances sont associées à des modes de rupture très différents associant la fibre, la résine ou l’interface fibre/résine. Ces modes de rupture peuvent être de type :
- Elastique fragile X,
- Micro-flambage X’,
- Ductile faiblement non linéaire Y ou fortement non linéaire Y’ et S.
Les stratégies de prévision des résistances ou déformations à rupture des composites sont donc très diverses de même que les modèles associés (CHAMIS, 1969). La complexité des modèles augmente si l’on ajoute les ruptures interlaminaires (dans l’épaisseur) telles que le cisaillement entre plis et la séparation entre plis (délaminage).
Dans le domaine des résines à fortes déformations, l’extension de la loi des mélanges permet de prévoir la résistance dans le sens des fibres X (TSAI, 1992). La résistance des fibres seules doit cependant être adaptée pour tenir compte de la dispersion et de l’effet de longueur. Les défauts de fabrication même faibles provoquent des écarts importants entre prévision et valeurs d’essai. Des écarts importants sont aussi présents pour les résines à faible déformation à rupture.
La rupture en compression dans le sens des fibres est liée à un phénomène de micro-flambage des fibres pouvant se dérouler suivant plusieurs modes (DOW et al., 1965). Les modèles existants de prévision de la résistance en compression sont basés sur des théories de stabilité en énergie de déformation (JONES, 1998). La prédictibilité de ces modèles est en général moyenne notamment pour les taux de fibres supérieurs à 50% où la statistique pourrait permettre d’expliquer les baisses de résistance. La complexité est augmentée par la très grande difficulté à réaliser des essais de compression pure sur des fibres.
Les ruptures de la résine ou de l’interface fibre/résine résultent d’un phénomène d’accumulation de microfissures. Les modèles de Chamis utilisent la notion de concentration de contrainte liée à la présence de la fibre dans un milieu continu (CHAMIS, 1969). Ces modèles ne tiennent pas compte de l’influence de l’épaisseur du pli ou de la présence des plis adjacents. Pour ces raisons, des prévisions par la mécanique de la rupture ont été développées (NAIRN, 2000) mais les paramètres matériaux ne sont pas facilement identifiables et la validation reste à réaliser. De plus, la détermination expérimentale des premières ruptures est très délicate.
La prévision de propriétés par la méthode du volume élémentaire représentatif VER s’est récemment trouvée améliorée dans le domaine de la rupture, de par les nouveaux développements de Sung Kyu HA (HA 2008), et ouvre une voie très cohérente appelée MMF (Micro-Mechanics of Failure).

Rail Shear Test
3 - Références bibliographiques :
BORNET M., BRETHEAU T. et GILORMINI P. Homogénéisation en mécanique des matériaux [Livre]. - [s.l.] : Hermes Science Publications, 2001.
CHAMIS C.C. Failure criteria for filamentary composites. Corporate Author : NATIONAL AERONAUTICS AND SPACE ADMINISTRATION WASHINGTON DC, AUG 1969.
CHRISTENSEN R.M. A Survey of and Evaluation Methodology for Fiber Composite Material Failure [Conférence]. - Chicago : 20th International Congress of Theoretical and Applied Mechanics,, 2000. - UCRL-JC-138787.
CHRISTENSEN R. M. « A critical evaluation for a class of micromechanics models ». J. Mech. Phys. Solids, 38 : 379-404, 1989.
COX et H.L. The Elasticity and strength of paper and other fibrous materials [Livre]. - [s.l.] : Brit J. Appl Phys, 1952. - Vol. 3.
DEUSCHLE H. Matthias3D Failure Analysis ofUD Fibre Reinforced Composites:Puck’s Theory within FEA, 2010, INSTITUT FÜR STATIK UND DYNAMIKDER LUFT- UNDRAUMFAHRTKONSTRUKTIONENUNIVERSITÄT STUTTGART
DIGIMAT brochure release 4.1.2 E-Xstream, mars 2011
DIGITIP L'industrie française des matériaux composites [Rapport] / Nodal consultant ; Ministère de l'économie, des finances et de l'industrie. - mai 2002.
DRAY BENSAHKOUM Delphine Prédiction des propriétés thermo-élastiques d'un composite injecté et chargé de fibres courtes [Livre]. - [s.l.] : Thèse ENSAM Mécanique et Matériaux, 2006.
ESHELBY JD The determination of the elastic field of an ellipsoidal inclusion and related problems [Revue]. - [s.l.] : Proc Roy Soc, 1957. - Vol. A.
GUILLEMINOT J. thèse Modélisation probabiliste des fluctuations des fractions volumiques dans les composites [Livre]. - ENSM Douai : [s.n.], 2008.
HA SUNG KYU, HUANG Y., JIN K.K. Effects of fiber arrangement on mechanical behavior of unidirectional composites, Strength and Life of composite, ed TSAI, 2008.
HA SUNG KYU, JIN, HUANG Micro-Mechanics of Failure for continuous fiber reinforced composites, Strength and Life of composite, ed TSAI, 2008.
HALPIN J.C. Stiffness and expansion estimates for orented short fiber composites [Revue]. - [s.l.] : Journal of composite materials, 1969. - Vol. 3.
HEON M. et SARTORIUS E. La politique française dans le domaine du calcul scientifique [Rapport] / Conseil général des technologies de l'information - Inspection générale de l'administration, de l'éducation nationale et de la recherche. - 2005.
IMBERT, J.F.; EADS Problématique et vision industrielle de la synergie essais-physiques essais virtuels [Conférence] // NAFEMS Synergie essais physiques-essais virtuels. - 2008.
JONES R. M. Mechanics of composite matérial - second edition [Livre]. - [s.l.] : Taylor and Francis, 1998.
KOLLAR P. LAZLO ET SPRINGER G. S. Mechanics of composite structures [Livre]. - [s.l.] : Cambridge university press, 2003.
KUMASAWA H., SUSUKI I. Gaz leakage evaluation of CFRP cross ply laminates under bi-axial loadings Journal of Composite Material vol 40 10/2006.
LADEVEZE P Multiscale Computational Damage Modelling of Laminated Composites, 2008, Course on Emerging Techniques for damage prediction and Failure Analysis of Laminted Composite Structures
Mc LAUGHLIN R. A study of the differential scheme for composite materials [Revue]. - [s.l.] : Internation Journal of Engineering Sciences, 1977. - Vol. 15.
Ministère de l'Ecologie de l'Energie, du développement durable et de l'Aménagement du territoire Synthèse sur les innovations et ruptures technologiques dans le domaine des transports à l'horizon de 10 à 25 ans. [Rapport] / Direction de la recherche et des affaires scientifiques et techniques. - 2003.
MAIRE Jean-François Endommagement : caractère unilatéral, anisotropie initiale et induite, conférence AUSSOIS 2011
MILITARY HANDBOK 17-3 volume 3.Polymer matrix composites materials usage, design, and analysis US Department of Defense.
MIYANO Y., NAKADA M. and CAI Formulation of long term creep and fatigue strength on ATM Strength and Life of Composites, Ed TSAI, 2008.
MORI T. et TANAKA K. Average stress in matrix and average elastic energy of materials woth misfitting inclusions [Revue]. - [s.l.] : Acta Metall, 1973. - Vol. 21.
NAIRN J.A. Matrix Microcracking in Composites - Polymer Matrix Composites, Chapter 13, R. Talreja and J-A.Manson, eds., in press (2000).
SHUECKER C. DAVILA C.G. and PETTERMAN Modelling the Non-linear Response of Fiber-Reinforced Laminates Using a Combined Damage/plasticity Model, 2008, NASA/TM-2008-215314
TSAI S. Theory of Composite Design [Livre]. - [s.l.] : Think Composites, 1992.
S. NEMAT-NASSER AND S. HORI. Micromechanics: overall properties of heterogeneous materials. North-Holland series in applied mathematics and mechanics, The Netherlands, 1993.
Z. HASHIN AND S. SHTRIKMAN. “A variational approach to the theory of the elastic behavior”.

