Composite : Characteristics
PREDICTING COMPOSITE MATERIAL CHARACTERISTICS
1 - Technical context
Composite materials stand out through a wide diversity in their behaviours born of an association of fibers and resin. The amount of fibers, the type of reinforcement and theirfiberorientation are determining elements that may lead to materials with completely different characteristics. It is therefore possible to obtain a rigid high performance material with a fragile elastic behaviour (like a beam made from pre-impregnated epoxy/carbon fibre) or a soft material that accepts large deformation (a cover made from a polyester/fiberglass chopped strand mast composite).

A Caron/Aramid/Glass reinforcement (source Saertex)
Composite materials are also unique in that they show anisotropy: a difference in behaviour depending on the direction from which strain is applied. This physical property significantly increases the number of parameters that determine rigidity, strength, thermal effects, etc. (generally there are at least three elasticity modulus, three Poisson's ratios and three shear moduli).
The number of possible combinations for manufacturing composite materials is practically infinite. Consequently, composite materials are bespoke developments or taylor designed.
These elements explain why any kind of standardization approach, one that exists for metal materials, has always been in vain for composite materials. In current design consultancy practice, the mechanical characteristics of composites are often derived from characterization test campaigns. Many long and costly characterization tests therefore need to be performed to develop composite materials that meet the specifications. Furthermore, in many cases, the characterization tests will only yield some of a material's characteristics. This is because some tests, like compression tests, are hard to implement and interpret.
To complement tests, or as an alternative to them, Méca has developed a prediction-based approach for the mechanical characteristics of composite materials.

Various parts made from composite materials
2 - State of the art in the field of micro-mechanics
2.1 - Methods for predicting mechanical characteristics
Changing from a microscopic scale to a macroscopic scale is one of the greatest mechanical challenges, but this is also the case in any field (optics, acoustics, etc.) that is a part of modern general physics. This is because the relationships linking atomic sequences to a structure’s macroscopic mechanical properties are not yet known. Nevertheless, the finest possible knowledge of a material's heterogeneity structure allows, through "phenomenological shortcuts" and "homogenization" processing, a way to determine a homogeneous macroscopic behaviour, likely to then be integrated into a conventional formulation of continuous environments (Guilleminot, 2008).

Real fibre arrangements and theoretical models
Homogenization techniques have been developed for composite materials. The aim is to determine the behaviour of a material created in this way from a knowledge of its microstructure (the fibre and resin taken alone). Two approaches coexist (Jones, 1998):
- The so-called micromechanical technique, where relationships are set out explicitly as rules or formulas;
- The so-called Representative Elementary Volume (REV) technique which is more general and based on a digital simulation, generally using the finite elements of an element that represents the material.
The foundations of homogenization techniques have been set out from a mathematical point of view (Nemat, 1993). The resolution of inclusion problems by John Eshelby in 1957 allowed this to be formally set out in tensorial form (Eshelby, 1957). "Hill's lemma", "Voigt and Reuss's upper and lower bounds" or, more recently, "Hashin and Shtrikman's bounds" (Bornet, et al., 2001) mean that predicted values can be bounded but this does not assess them.
Furthermore, the REV technique requires a high number of micro-components that have to be statistically representative of continuous local properties (Guilleminot, 2008), and this is very difficult to define and obtain.
2.2 - Forecasting the rigidity characteristics of composite materials
Existing models used to forecast material rigidity characteristics are generally based on simple and reproducible geometries (UD or unidirectional, short fibre and spherical inclusion).
2.2.1 - Long fibre case
Cox Model
In the first model for forecasting rigidity along the fibre strand direction (Kollar, et al., 2003), the fibre and the resin are defined as two springs that may act in line with a serial or parallel model. The load transfer takes place through shearing in line with the Shear Lag model (Cox, et al., 1952). In this case, the fibers are said to be long and continuous. The first order prediction for the elasticity modules for unidirectional type layers in structural composites broadly obeys this law(with a -10% deviation from the module in the fibre direction for aeronautical type composites). In the transverse fibre direction, semi-empirical laws have been developed by Halpin-Tsai to allow a better forecast to be obtained for transverse elasticity, shear and Poisson’s ratio (Halpin, 1969). The predictability of these models is low, especially for high fibre ratios where the models overestimate the transverse modules for fibers across their thickness.
2.2.2 - Short fibre case
For short fibers with only a low reinforcing ratio (particularly used for plastic injection), rigidities may be assessed from the Mori Tanaka model (Mori, et al., 1973). The Lielens model (Dray Bensahkoum, 2006) is used to improve predictions for high concentrations (typically 40 to 60%).
It is also possible to use developments around Eshelby's method, using various assumptions as to the environment of reference: diluted schema, auto-coherent schema and the differential model (McLaughlin, 1977). The latter consists of successively adding a low density fraction of reinforcement to the homogenized material until the real fraction is obtained in the composite.
REV homogenization techniques are currently finding a second wind thanks to the work done by Ha (Ha and Huang, 2008). They systematized the finite element calculation on REVs. They include a large number of fibers coupled with the Miyano approach (Miyano, 2008) of forecasting creep and temperature characteristics from data measured from the resin alone.
Any improvement in the predictability of the model requires better allowance for the physical reality of the way the reinforcing and the matrix is organized in relation to a geometric and mathematic idealization. It is therefore necessary to study the way the following are handled:
- Porosities or voids
- Manufacturing related restrictions
- Reinforcements misalignments
- Micro-defects (microcracking), etc.
In the field of short fibre injected polymers, major advances have been achieved in the use of the REV technique and the Mori-Tanaka model working with the Digimat software suite (Digimat 2011). Interfacing with rheology and calculation software has been achieved. The initial feedback shows that these approaches yield highly satisfactory results when it comes to forecasting rigidity characteristics (Dray Bensahkoum, 2006) with however a resolution time that has still to be optimized.
When it comes to predicting failure characteristics, the approaches are currently qualitative only and have still to be developed.
2.2.3 - Non linearbehaviour
Non-linear behaviour of composite materials is mainly observed as shearing along the plane and in transverse compression. It is important to know these evolutions so as to reproduce the stress redistribution phenomena until failure occurs.
The current approach comes from damage mechanics (Maire 2011). The way the modules evolve is then linked to that of damage which may be viewed in the form of microcracks, for example. In its simple, non-coupled version the Chaboche type model is found or, in its more refined evolution, that of the work done by Ladeveze (Ladeveze 2008).
The semi-empirical approach to changes in the transverse rigidity of a composite under shear or traction linked to Puck criteria (Deuschle 2010) is a promising area as it forms a highly coherent set of methods and tools.
Recent experimental works have highlighted that non-linearities, especially in terms of shear, were not only caused by microcracking but also comprised a degree of plasticity. Coupled models combining damage mechanics and plasticity are currently being developed (Shuecker 2008).
2.3 - Forecasting the strenght characteristics of composite materials
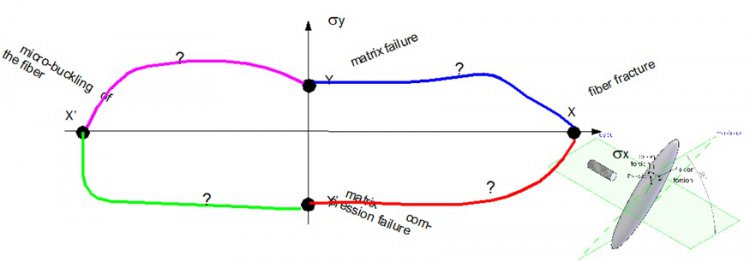
Failure envelope - unidirectional layer of long fibers
The characteristics of the first failures to be determined for a laminate composite with a plane stress type behaviournumber five in total(Christensen, 1989):
- Strength along the fiber direction, X in traction and X’ in compression;
- Transverse fiber resistance levels in fibers, Y in traction, Y’ in compression and shear along the S plane.
These resistance values are assigned to very different failure modes associating fibre, resin and the fibre/resin interface. These failure mode types may be:
- Elastic fragile X;
- Micro-buckling X’;
- Ductile slightly non-linear Y or significantly non-linear Y’ and S.
The strategies for forecasting strength or deformation at failure point for composites are therefore highly diverse as are the related models(Chamis, 1969). The complexity of the models increases if we add the failures between laminae (through the thickness of the material) like shear between plies and separations between plies (delamination).
Regarding resins with large deformations, an extension of the mixing law means that resistance along the X fibre direction can be predicted (Tsai, 1992). The resistance of the fibers alone must however be adapted to take into account dispersion and the length effect. Even minor manufacturing defects cause significant deviations between forecast and actual test values. Significant deviations are also present for resins with only a slight deformation prior to failure.
A compression failure along the direction of the fibers is linked to a fibre micro buckling phenomena that may occur in a number of modes (Dow et al., 1965). The existing models used to forecast compression strength are based on stable deformation energy theories (Jones, 1998). The predictability of these models is generally only average, especially for fibervolume contents in excess of 50% where statistics may be able to explain the fall in resistance. The complexity is increased by it being very hard to perform pure compression tests on fibers.
Failures affecting the resin or the fiber/resin interface are the result of a microcrack build-up phenomenon. The Chamis models use a stress concentration concept linked to the presence of the fiber in a continuous environment (Chamis, 1969). These models do not take into account the influence of the thickness of the plies or the presence of adjacent folds. For these reasons, forecasts using failure mechanics have been developed (Nairn, 2000) but the material parameters are not easy to identify and validation has yet to be performed. Furthermore, an experimental determination of the first failures is very delicate to achieve.
Predicting properties using the REV representative elementary volume method has recently been improved as regards failures thanks to new developments by Sung Kyu HA (Ha 2008), and this opens a highly coherent path called MMF (Micro-Mechanics of Failure).

Rail Shear Test
3 - Bibliography
BORNET M., BRETHEAU T. et GILORMINI P. Homogénéisation en mécanique des matériaux [Livre]. - [s.l.] : Hermes Science Publications, 2001.
CHAMIS C.C. Failure criteria for filamentary composites. Corporate Author : NATIONAL AERONAUTICS AND SPACE ADMINISTRATION WASHINGTON DC, AUG 1969.
CHRISTENSEN R.M.A Survey of and Evaluation Methodology for Fiber Composite Material Failure [Conférence]. - Chicago : 20th International Congress of Theoretical and Applied Mechanics,, 2000. - UCRL-JC-138787.
CHRISTENSEN R. M. « A critical evaluation for a class of micromechanics models ». J. Mech. Phys. Solids, 38 : 379-404, 1989.
COX et H.L.The Elasticity and strength of paper and other fibrous materials [Livre]. - [s.l.] : Brit J. ApplPhys, 1952. - Vol. 3.
DEUSCHLE H. Matthias 3D Failure Analysis of UD Fibre Reinforced Composites: Puck’s Theory within FEA, 2010, INSTITUT FÜR STATIK UND DYNAMIK DER LUFT- UND RAUMFAHRTKONSTRUKTIONEN UNIVERSITÄT STUTTGART
DIGIMAT brochure release 4.1.2 E-Xstream, mars 2011
DIGITIP L'industrie française des matériaux composites [Rapport] / Nodal consultant ; Ministère de l'économie, des finances et de l'industrie. - mai 2002.
DRAY BENSAHKOUM Delphine Prédiction des propriétés thermo-élastiques d'un composite injecté et chargé de fibres courtes [Livre]. - [s.l.] : Thèse ENSAM Mécanique et Matériaux, 2006.
ESHELBY JD The determination of the elastic field of an ellipsoidal inclusion and related problems [Revue]. - [s.l.] :Proc Roy Soc, 1957. - Vol. A.
GUILLEMINOT J. thèse Modélisation probabiliste des fluctuations des fractions volumiques dans les composites [Livre]. - ENSM Douai : [s.n.], 2008.
HA SUNG KYU, HUANG Y., JIN K.K. Effects of fiber arrangement on mechanical behavior of unidirectional composites, Strength and Life of composite, ed TSAI, 2008.
HA SUNG KYU, JIN, HUANG Micro-Mechanics of Failure for continuous fiber reinforced composites, Strength and Life of composite, ed TSAI, 2008.
HALPIN J.C. Stiffness and expansion estimates for oriented short fiber composites [Revue]. - [s.l.] : Journal of composite materials, 1969. - Vol. 3.
HEON M. et SARTORIUS E. La politique française dans le domaine du calcul scientifique [Rapport] / Conseil général des technologies de l'information - Inspection générale de l'administration, de l'éducation nationale et de la recherche. - 2005.
IMBERT, J.F.; EADS Problématique et vision industrielle de la synergie essais-physiques essais virtuels [Conférence] // NAFEMS Synergie essais physiques-essais virtuels. - 2008.
JONES R. M. Mechanics of composite matérial - second edition [Livre]. - [s.l.] : Taylor and Francis, 1998.
KOLLAR P. LAZLO ET SPRINGER G. S. Mechanics of composite structures [Livre]. - [s.l.] : Cambridge university press, 2003.
KUMASAWA H., SUSUKI I. Gaz leakage evaluation of CFRP cross ply laminates under bi-axial loadings Journal of Composite Material vol 40 10/2006.
LADEVEZE P Multiscale Computational Damage Modelling of Laminated Composites, 2008, Course on Emerging Techniques for damage prediction and Failure Analysis of Laminted Composite Structures
Mc LAUGHLIN R.A study of the differential scheme for composite materials [Revue]. - [s.l.] :International Journal of Engineering Sciences, 1977. - Vol. 15.
Ministère de l'Ecologie de l'Energie, du développement durable et de l'Aménagement du territoire Synthèse sur les innovations et ruptures technologiques dans le domaine des transports à l'horizon de 10 à 25 ans. [Rapport] / Direction de la recherche et des affaires scientifiques et techniques. - 2003.
MAIRE Jean-François Endommagement : caractère unilatéral, anisotropie initiale et induite, conférence AUSSOIS 2011
MILITARY HANDBOOK 17-3 volume 3.Polymer matrix composites materials usage, design, and analysis US Department of Defense.
MIYANO Y., NAKADA M. and CAI Formulation of long term creep and fatigue strength on ATM Strength and Life of Composites, Ed TSAI, 2008.
MORI T. et TANAKA K. Average stress in matrix and average elastic energy of materials wothmisfitting inclusions [Revue]. - [s.l.] :ActaMetall, 1973. - Vol. 21.
NAIRN J.A. Matrix Microcracking in Composites - Polymer Matrix Composites, Chapter 13, R. Talreja and J-A.Manson, eds., in press (2000).
SHUECKER C. DAVILA C.G. and PETTERMAN Modelling the Non-linear Response of Fiber-Reinforced Laminates Using a Combined Damage/plasticity Model, 2008, NASA/TM-2008-215314
TSAI S. Theory of Composite Design [Livre]. - [s.l.] : Think Composites, 1992.
S. NEMAT-NASSER AND S. HORI. Micromechanics: overall properties of heterogeneous materials. North-Holland series in applied mathematics and mechanics, The Netherlands, 1993.
Z. HASHIN AND S. SHTRIKMAN. “A variational approach to the theory of the elastic behavior”.

